Then, how do we get or calculate a prognostic score $\psi(X)$? The original work says it depends on the assumed model regarding the covariates and the outcomes rather than just on covariates and outcome data. Furthermore, it assumes $\psi(X)$ is a scalar. However, it is not always the case; consider $Y = (X_1 + \epsilon_1)(X_2 + \epsilon_2)$, where $\epsilon_1$ and $\epsilon_2$ are independent noises. As conditioning only one of $X_1$ or $X_2$ does not specify the distribution of $Y$, $\psi(X)$ cannot be a one-dimensional value.

To resolve these issues, we devised a data-driven method to estimate a multi-dimensional prognostic score. The main idea of this procedure is the following two steps:

• Decompose $X$ into independent components,
• Choose components most relevant to $Y$ among those.

We use the independent component analysis (ICA) for the first step. I learned it while studying causal discovery; ICA is one prominent approach for causal discovery, including the seminal work LinGAM. ICA assumes the sources are non-Gaussian, so we need the same assumption here.

For the second step, we use mutual information. It indicates the amount of information two variables share, so we sort components by mutual information of them and $Y$ in descending order and take the first few of them. This process has a drawback in that we should select the number of independent components to be chosen. We may change how to choose the relevant components; for example, we can threshold mutual information.

To verify our method, we calculated the average treatment effect on the treated (ATT) by using the estimated prognostic score.

You can check out our final report Final Report.

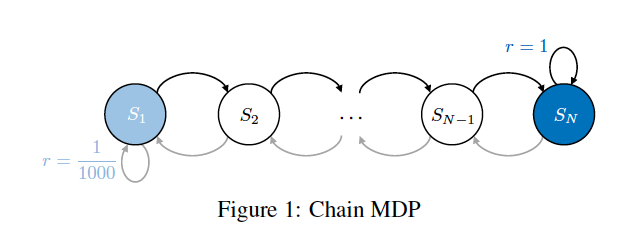
In this problem, there are $N$ states forming a chain, as in the above figure. The agent can take two actions at each step: going left ($L$) or right ($R$). At the most left state, the agent gets a reward of 1/1000 by taking $L$. In contrast, the agent gets a bigger reward of 1 by taking $R$ at the most right state. We aim to maximize the cumulative reward in a fixed number of steps.

The main difficulty of this problem is that the agent sticks to getting the small reward repeatedly, as exploring rightward states do not give any reward until it reaches the rightmost state. Bootstrapped DQN resolves this problem by boosting exploration. In brief, it uses multiple DQN agents and chooses one of the DQN agents at each episode to take greedy action with respect to the Q values the agent outputs. Then a pair of (state, action, reward, next state) is saved in the replay buffer to update each DQN agent, with their magnitude controlled by masks at each step.

However, we cannot maximize the cumulative reward by choosing the DQN agent at each step for determining actions; after the agent recognizes the whole reward structure through enough exploration, we need to exploit such information. I added an ‘exploit DQN agent’ to resolve this issue. This agent learns the reward structure consistently, and we start exploiting the agent when there is a signal of perfectly learning the reward structure.

After fine-tuning, our novel agent started to perform very well. You can check out more details in following files: Term project report, PyTorch implementation.

I have implemented a few techniques to parallelize transposed convolution. First, I have reduced unnecessary divergence(if-branches) to make the code friendly with the lock-step architecture of GPUs; since all streaming cores in a warp fetch instructions both from true and false blocks, including many if-branches, become overhead to the program.

Second, I tried to express transposed convolution as (massive) matrix multiplication. The motivation for this was that matrix multiplication is highly parallelizable. There are extremely fast matrix multiplication algorithms; thus, I would benefit from those if I regard transposed convolution as matrix multiplication. Designing and implementing this notion was very painful: building and reshaping the matrix in C was confusing, and debugging CUDA codes without using printf (which I thought I could not use in GPUs) was vastly time-consuming. Mainly, the arcane behaviors of C language macro fooled me; it made me waste a day debugging my code.

Going through these efforts, I could largely shorten the process of transposed convolution. The initial sequential CPU implementation of the method was excruciatingly long: it took longer than 1 minute to generate a single artificial face portrait. So, in theory, it would have taken longer than 16 hours to generate 1000 faces. However, implementing the generator in CUDA GPUs essentially shortened the process: I ended up with the project generating 1000 faces in under 0.2 seconds. With 5000 times boost in the process, I was pleased about how far computing technology would enhance human lives. It will take humankind to the level we could never reach without computers!

You can check out my term project report: Term project report(in Korean), Term project report(in English).